Reading about probabilistic programming, I often come across the notion of confidence intervals around a regression curve, the idea being that the larger the interval around the curve, the less “certain” we are about the function’s “true” value at that point. For example:
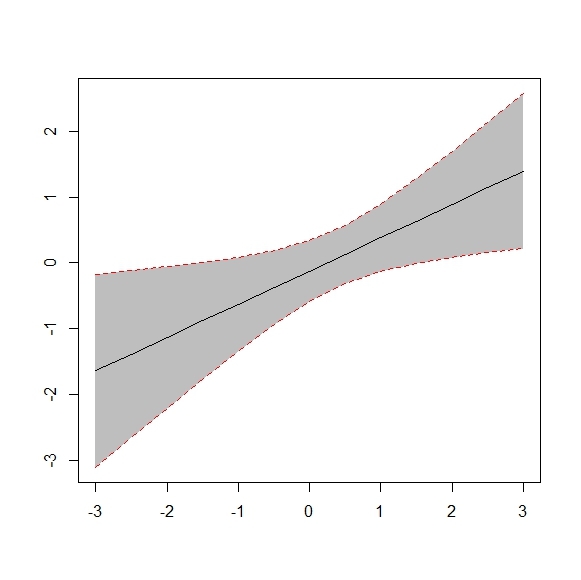
However I can’t for the life of me figure how to produce something similar in Edward. I read the criticism tutorial and API docs and I know about PPC, but it doesn’t seem quite the same thing.
Frequentist methods to get confidence intervals in Edward work in the same way you might imagine doing it. E.g., bootstrap the data, fit your model on each bootstrapped data set, then take quantiles over the set of parameter estimates. Or fit your point estimate with maximum likelihood, then calculate asymptotic variances through the usual closed-form formulas.
The Bayesian equivalent is known as a credible interval. Namely, draw samples from the posterior, then take the 2.5th and 97.5th quantiles. This defines a 95% credible interval. This can be done to get error bars on parameter estimates, or also just error bars on your predictions as you do in PPCs. (This is what the Bayesian neural net does in the getting started example.)
