Hello there
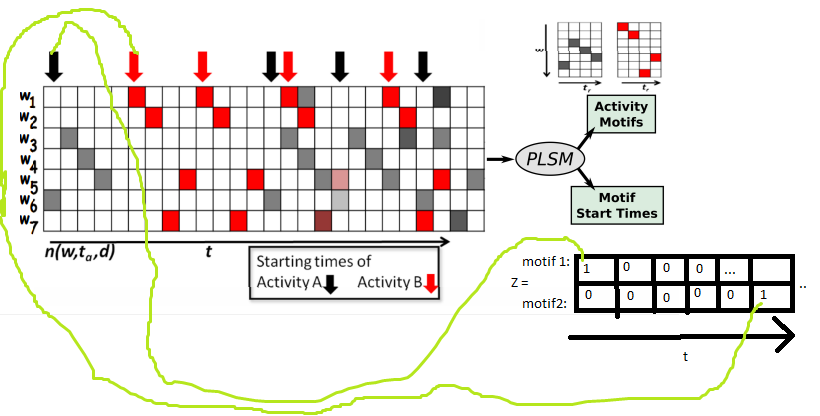
Given a set of documents (which are the big array in the image), i’m trying to infere z and the motifs (colors should be numbers and the more the color rate the higher the number, also z and motifs should be normalized to sum up to one).
I’m trying first to infere z, here snippet of my code (note that i convert my documents from array to big vector so my data = set of documents is finally a set of vectors):
I set z as a Dirichlet:
session = ed.get_session()
z = Dirichlet(tf.constant([[1.0,2.0,3.0,4.0,5.0,6.0,4.0,4.5,2.5,1.0], [1.0,2.0,3.0,6.4,5.0,1.3,4.0,2.5,4.5,1.0], [8.0,2.3,3.2,4.0,1.0,1.0,4.0,3.5,2.5,1.0]]), name='z')
I define motifs and function that will return my data:
def normalize(array):
return z/np.sum(array)
A=np.matrix('1,3,1,5,5; 1,1,0,0,0')
B=np.matrix('1 1 0 0 0; 0 4 30 1 0')
C=np.matrix('1 1 20 10 0; 0 4 1 1 0; 2 0 0 5 5')
motif1=normalize(A)
motif2=normalize(B)
motif3=normalize(C)
motifs = [motif1,motif2,motif3]
Nz=len(motifs)
guess_Ts=[]
for i in motifs:
guess_Ts.append(np.shape(i)[0])
Ts=max(guess_Ts)
def expect(RV):
rows=RV.eval().shape[0]
cols=RV.eval().shape[1]
RV_expect = np.zeros((rows,cols))
for _ in range(10000):
RV_expect = RV_expect + RV.eval()
RV_expect = RV_expect/10000
return tf.constant(RV_expect)
def generate_one_doc(z,motifs):
Nz=z.shape[0]
Td=z.shape[1]
doc=np.zeros((Td,5))
for j in range(Td-Ts+1):
for i in range(Nz):
for k in range(motifs[i].shape[0]):
for l in range(motifs[i].shape[1]):
doc[j+k,l]=doc[j+k,l]+z.eval()[i,j]*motifs[i][k,l]
return doc
def generate_set_of_docs(z,motifs):
data=[]
for i in range(10):
data.append(generate_one_doc(z,motifs).ravel().tolist())
return tf.constant(data)
Model:
data=generate_set_of_docs(expect(z),motifs)
w=generate_set_of_docs(z,motifs)
qz = Dirichlet(tf.nn.softplus(tf.Variable(tf.ones([3,10]))), name="qz")
Inference:
inference = ed.KLqp({z: qz}, data={w: data})
inference.initialize()
inference.n_iter = 10000
tf.global_variables_initializer().run()
for _ in range(inference.n_iter):
info_dict = inference.update()
inference.print_progress(info_dict)
inference.finalize()
The code works more or less pretty well in that form, though sometimes that doensn’t infer.
The problem is that if I replace my initial z Dirichlet with one which have lot of zeros in parameters (this is what I want), like that :
z = Dirichlet(tf.constant([[5.0,0.0,0.0,1.0,0.0,0.0,1.0,1.0,0.0,0.0], [0.0,1.0,0.0,5.0,1.0,0.0,0.0,0.0,0.0,0.0], [0.0,1.0,0.0,0.0,5.0,0.0,1.0,0.0,0.0,5.0]]), name=‘z’)
The inference doesn’t work…
If I define the motifs as Dirichlet instead of numpy arrays, in order to infer them, as I do for z: that doesn’t work neither…
Does someone have an idea ?