Loss increasing in inference of Poisson Factorization

1

I am try to implement a simple Poisson Factorization

theta ~ Gamma(a, b)
beta ~ Gamma(c, d)
x ~ Poisson( theta . beta )

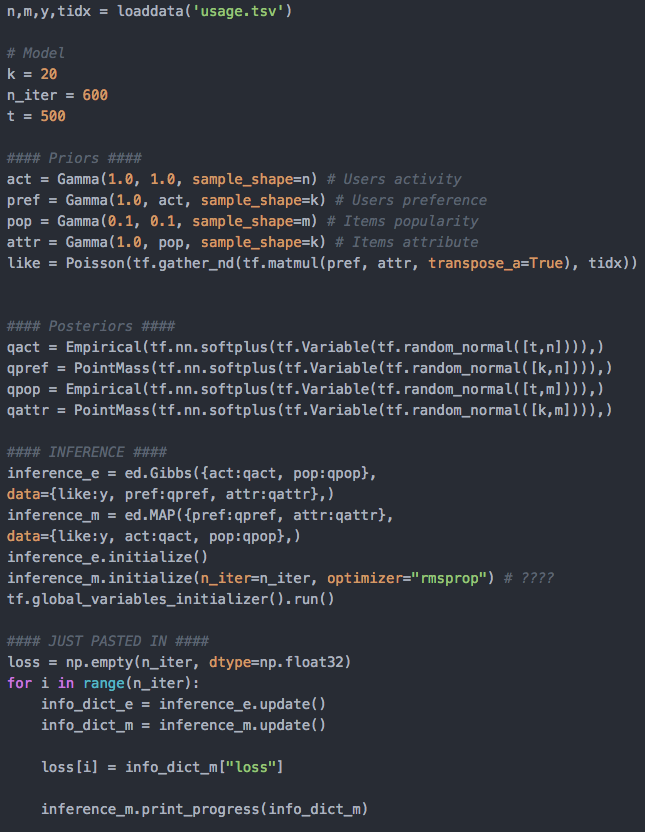
My codes:

from edward.models import Poisson, Gamma
import edward as ed

# Toy dataset
M = (np.random.random((300,200))>0.9).astype(int)

# Model
theta = Gamma(1.*tf.ones([300, 10]), 1.)
beta = Gamma(1.*tf.ones([200, 10]), 1.)
X = Poisson(tf.matmul(theta, tf.transpose(beta)))

# Inference
q_theta = Gamma(tf.nn.softplus(tf.Variable(tf.random_normal([300, 10]))),
                tf.nn.softplus(tf.Variable(tf.random_normal([300, 10])))) 
q_beta = Gamma(tf.nn.softplus(tf.Variable(tf.random_normal([200, 10]))),
               tf.nn.softplus(tf.Variable(tf.random_normal([200, 10])))) 

# Inference
inference = ed.KLqp({theta: q_theta, beta: q_beta}, data={X: M})
inference.initialize(n_print=30, n_iter=300)
tf.global_variables_initializer().run()
for t in range(inference.n_iter):
    info_dict = inference.update()
    inference.print_progress(info_dict)
    if t % inference.n_print == 0:
        print '\tloss: %f'%info_dict['loss']

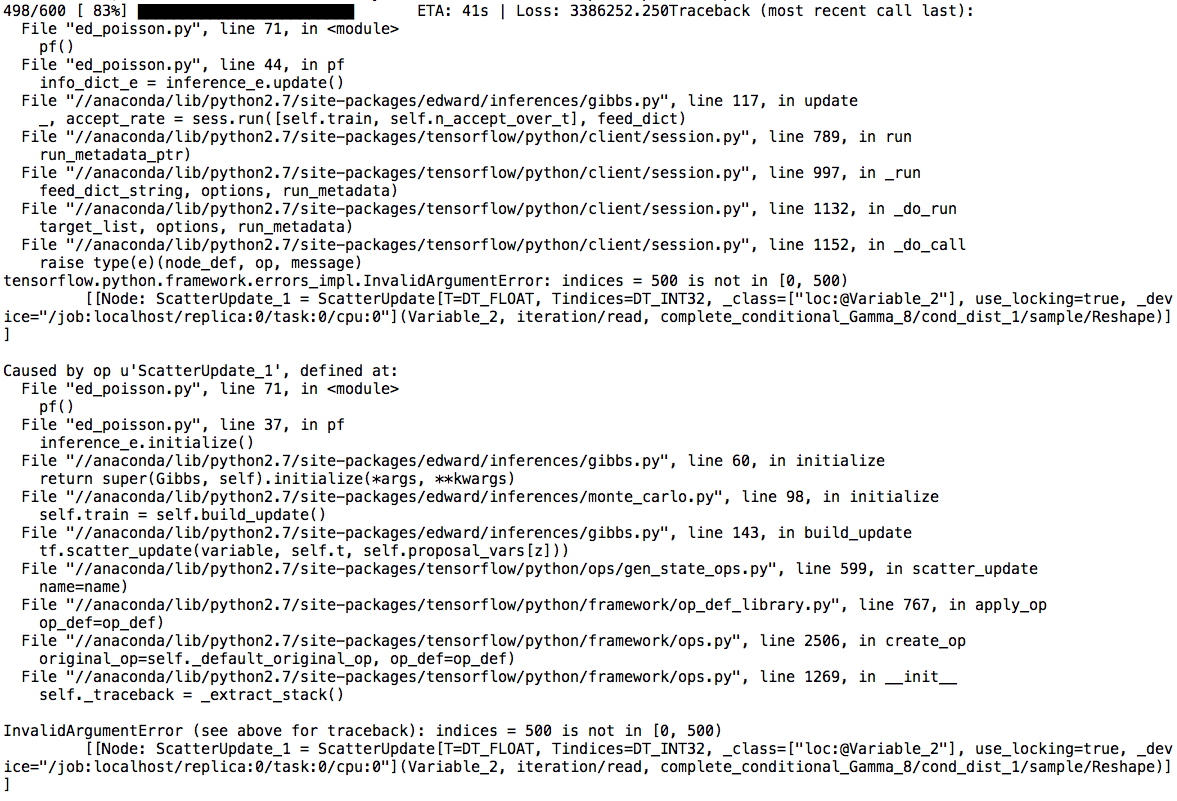
Why I got the increasing loss? and ended up nan

1/300 [ 0%] ETA: 743s | Loss: 1969714.125 loss: 1969714.125000
30/300 [ 10%] ███ ETA: 23s | Loss: 5959987.500 loss: 5910604.000000
60/300 [ 20%] ██████ ETA: 10s | Loss: 27670352.000 loss: 29153144.000000
90/300 [ 30%] █████████ ETA: 6s | Loss: 335439648.000 loss: 430829216.000000
120/300 [ 40%] ████████████ ETA: 4s | Loss: 5386785280.000 loss: 5760766464.000000
150/300 [ 50%] ███████████████ ETA: 2s | Loss: 88767381504.000 loss: 92775710720.000000
180/300 [ 60%] ██████████████████ ETA: 1s | Loss: nan loss: nan
210/300 [ 70%] █████████████████████ ETA: 1s | Loss: nan loss: nan
240/300 [ 80%] ████████████████████████ ETA: 0s | Loss: nan loss: nan
270/300 [ 90%] ███████████████████████████ ETA: 0s | Loss: nan loss: nan
300/300 [100%] ██████████████████████████████ Elapsed: 3s | Loss: nan

2

ed.KLqp fares poorly on Gamma latent variables. For scalable Poisson factorization, I recommend EM algorithms such as the one used by @dadaromeo: https://github.com/dadaromeo/recsys-hpf.

3

Thanks I will give that a try.

4

Hi JHChen and Dustin,

I’ve been working on Edward model for Poisson factorization with Gamma latent variable using ed.Kqp. I wasn’t getting “nans” for the loss. However, my predictions weren’t right. I’ll also look into EM algorithm as well.

Best,
Mark

5

Hi Dustin. I’ve run @dadaromeo’s EM algorithm on my own data. Works fine out-of-the-box, but if I change the number of iterations then I get the following error. Any chance you could explain what the error means? The number of iterations was originally set to 500, and if I increase it beyond 500 it appears to fail when it reaches 500…

6

Hi Matthew,

How did you setup the inference procedure for the Poisson Factorization using EM algorithm in Edward?

Best,
Mark

7

Hi mac. My code is below.

8

*Mark. Sorry …

9

In the algorithm you set the Empirical approximation as holding t=500 samples. If n_iter is greater than t, then the Empirical approximation cannot hold any more samples so the error is raised.

10

Hi Matthew,

Thank you. It was instructive!

11

Thank you very much for the support that you’ve given across this forum. Would you mind expounding on exactly why KLqp fares poorly on Gamma latent random variables? More generally, when will KLqp fare poorly and what is the fundamental cause? Or perhaps could you point to a resource that will explain the issue? Thanks!