What's the suggested way to generate and examine posterior distributions of parameters?

1

PyMC3’s “trace” object and “traceplot” function are pretty handy to examine the posterior distributions.
Q1: What’s the suggested way to do in Edward?

I couldn’t find a reference, so below is what I do currently:

# Use a simple linear regression as an example:
import pandas as pd
import numpy as np
import tensorflow as tf
import edward as ed

def generateData(intercept=1, slope=3, noise=1, n_points=20):
    df = pd.DataFrame({'x': np.random.uniform(-3, 3, size=n_points)})
    df['y'] = intercept + slope * df['x'] + np.random.np.random.normal(0, scale=noise, size=n_points)
    df = df.sort_values(['x'], ascending=True).reset_index(drop=True)
    return df

intercept = 1; slope = 3; noise = 1
np.random.seed(99)
data = generateData(intercept=intercept, slope=slope, noise=noise)  #, n_points=n_points)

# 
N = 20
D = 1
X = tf.placeholder(tf.float32, [N, D])
sigma = ed.models.Chi2(df=3.0)
w = ed.models.Normal(loc=tf.zeros(D), scale=tf.ones(D)*10.0)
b = ed.models.Normal(loc=tf.zeros(1), scale=tf.ones(1)*10.0)
y = ed.models.Normal(loc=ed.dot(X, w)+b, scale=tf.ones(N)*sigma)

T = 10000

qs = ed.models.Empirical(params=tf.Variable(tf.ones(T)))
qw = ed.models.Empirical(params=tf.Variable(tf.random_normal((T, D) )))
qb = ed.models.Empirical(params=tf.Variable(tf.random_normal((T, 1) )))

inference = ed.HMC({sigma: qs, w: qw, b: qb}, 
                   data={X: data[['x']].values, y: data['y'].values})
inference.run(step_size=3e-3)

# After the inference process is finished, generate posterior samples
n_samples = 1000
w_posterior = qw.sample(n_samples).eval().ravel()
b_posterior = qb.sample(n_samples).eval().ravel()
s_posterior = qs.sample(n_samples).eval().ravel()

The posterior distributions of the above three parameters are as follow:

50 PM

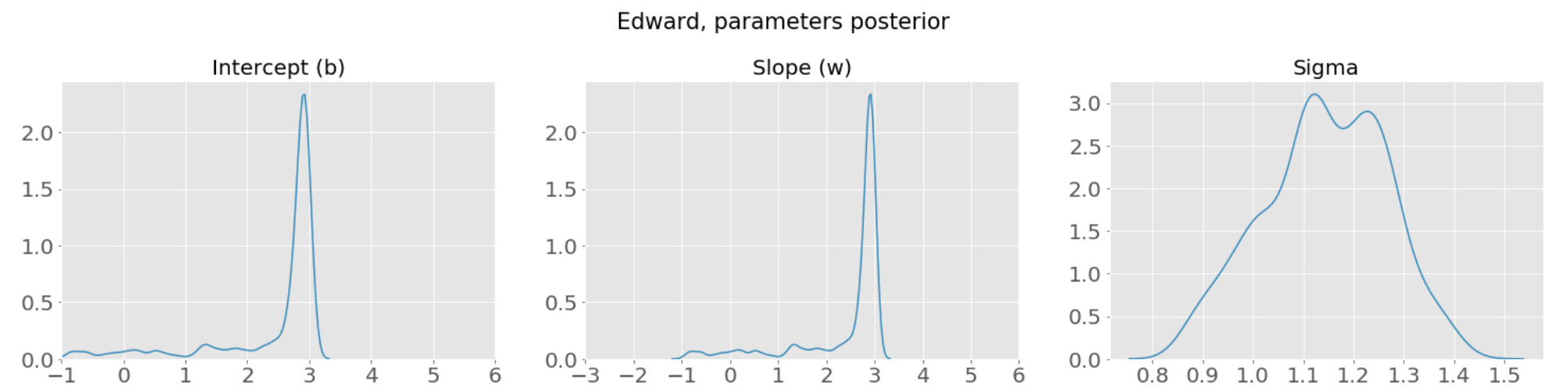
Q2: Is there a way to get the posterior samples from the “inference” object? It seems a bit awkward that I specified “T=10000” for the MCMC runs but I wasn’t able to use the samples there, and had to generate extra “n_samples = 1000” samples to examine the posteriors.

I’m new to Edward, so any suggestions are welcome and appreciated!

2

Your approach for examining HMC output is sensible if you believe that all the samples collected in Empirical are truly from the stationary distribution (posterior). If you’d just like the last 1000 samples, it’s recommended you grab them explicitly from the params of Empirical: qz.params[-1000:].

See examples/bayesian_linear_regression.py.

3

Got it, thanks @dustin!